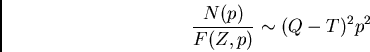Determinar, si es posible, el valor de Q a partir del espectro
experimental mediante el diagrama de Fermi-Kurie, ecuación (9.27) del
Krane:
Incluir las barras de error 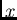 e
e 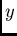 de los
datos experimentales en el diagrama. Supóngase que es una transición
permitida.
de los
datos experimentales en el diagrama. Supóngase que es una transición
permitida.
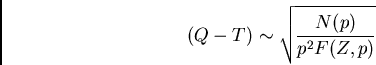
![]() e
e ![]() de los
datos experimentales en el diagrama. Supóngase que es una transición
permitida.
de los
datos experimentales en el diagrama. Supóngase que es una transición
permitida.